|
||||
Les machines du Docteur Roth (1800-1885) |
||||
Roth donne ici le détail d'une multiplicatrice plus simple et moins coûteuse que sa superbe multiplicatrice circulaire à nombre variable de dents.
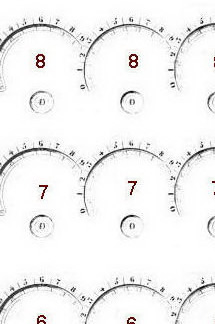
Il a rajouté à chaque cadran de son additionneur des rouages qui forment une série d'engrenages continus. Au dessus de chaque cadran ont été disposés verticalement 8 autres cadrans reliés mécaniquement par des pignons, afin que ceux-ci tournent dans le même sens, et dont la particularité est que leur vitesse augmente progressivement de bas en haut d'un dixième.
En somme, lorsque le cadran du haut (des 9) aura fait un tour, le cadran des 8 en aura fait 2, etc ..., et le cadran de l'additionneur (totalisateur) en aura fait 9.
Comme celui-ci possède un mécanisme de retenue, le résultat obtenu sera 81.
On n'a pas retrouvé pour l'instant de prototype complet de cette machine, mais le CNAM en possède un petit morceau. Même s'il est incomplet et si des pièces ont été mal repositionnées, on peut se faire une idée très précise de la machine.
Imaginons là avec un capacité de 8 chiffres. Elle possède alors un total de 72 cadrans !!! ce qui n'est pas rien à fabriquer tout de même !
Pour chaque décade: on a donc 9 cadrans. Le cadran inférieur est le cadran totalisateur de l'additionneur. Les autres correspondent aux multiples de 2,3,4,5,6,7,8, et 9.
Sous la platine, on a pour chaque multiple une "roue cadran" de 20 dents, muni d'un ressort sautoir, portant la numérotation 0.1.2.3.4.5.6.7.8.9. 0.1.2.3.4.5.6.7.8.9, deux roues d'engrenage superposées de 90 dents pour le multiple 9, 2 roues de 80 dents pour le multiple 8, etc .Ces roues d'engrenage ont été doublées pour une question de résistance probablement. Des pignons intermédiaires, doublés eux aussi, vont porter un nombre de dents inversement proportionnel aux roues d'engrenages afin de préserver l'égale distance entre chaque cadran.
Note de Michel Bardel
" La difficulté avec la machine à 72 cadrans, c'est que l'effort pour faire tourner le cadran le plus lent est 38 fois plus grand que celui du cadran le plus rapide. Ca explique qu'il ait dû doubler certains pignons pour encaisser l'effort.
La théorie de la conservation du travail veut que l'angle de rotation multiplié par le couple reste constant dans tout le mécanisme, donc, si une roue tourne 10 fois moins vite, son couple est dix fois plus fort. Dans le cas présent, il faut ajouter au couple de la roue la plus lente, deux fois celui de la suivante, plus trois fois celle d'après, plus quatre fois... etc.... le total fait 38.
A moins que les roues ne tournent sans effort, avec des pivots extrêmement bien huilés, ça me semble infaisable. Je ne compte pas les efforts des reports qui, eux aussi, sont multipliés.
C'était un abandon prévisible. Il n'a pas dû aller plus loin."
B) Multiplicateur et diviseur à réglettes
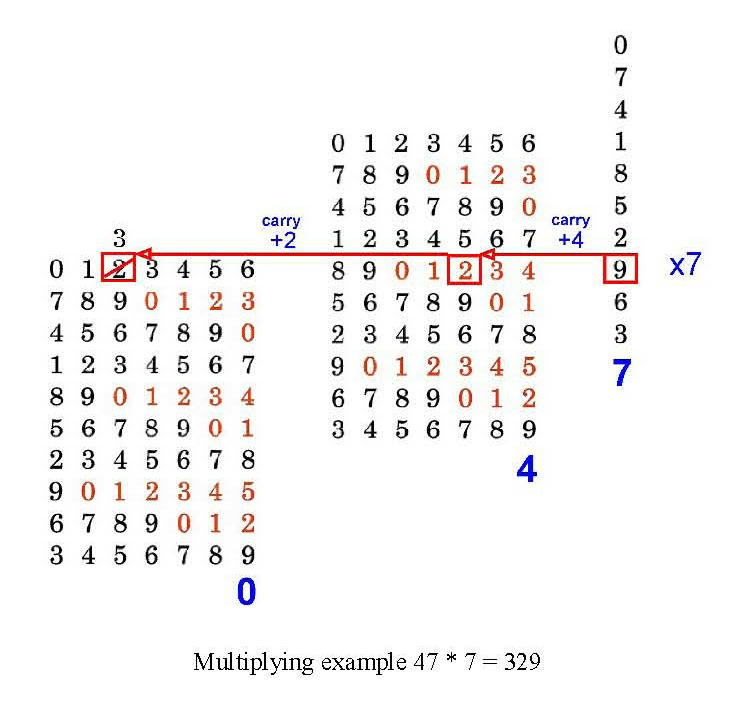
Roth a imaginé un système de multiplicateur / diviseur à réglettes très ingénieux. Dans cette nouvelle disposition, neuf séries de chiffres superposés verticalement sont imprimées sur une règlette en papier cartonné. Ils donnent le multiple de chaque chiffre de 1 à 9. L'instrument, qui a une capacité de 6 chiffres, contient 6 réglettes qui se chevauchent partiellement. De petites découpures judicieusement positionnées laissent apparaître "l'excès de transmission de l'unité sur la dizaine". Il s'agit en somme,si cela est nécessaire, de répartir le produit de la mutiplication d'un chiffre par un autre sur deux ordres décimaux.*1
Les réglettes sont placées dans un cadre en bois muni de 9 lucarnes horizontales (pour chaque multiple).
La platine inférieure possède six rainures verticales munies de curseurs permettant de déplacer les réglettes de bas en haut selon un ordre allant de 0 à 9.
Si, par exemple, on introduit le nombre 123456 à l'aide des curseurs, on verra apparaître au "deuxième étage" le produit de 123456 par 2, soit 246912, au "troisième étage" le produit de 123456 par 3 soit 370368 et ainsi de suite jusqu'au produit de 123456 par 9, soit 1111104, au 9ème étage !*2
B) Construction d'une réplique du multiplicateur à réglettes de Roth
Si l'idée vous tente d'en construire une réplique, voici quelques photos qui vous permettront d'en comprendre le principe. Il vous suffit d'imprimer en six exemplaires la réglette complète que je vous ai préparée. Il vous faudra les coller sur du carton dur mais pas trop épais car les réglettes se chevauchent et doivent coulisser les unes sur les autres sous l'effet du stylet. Pour caler l'ensemble, de petites baguettes de bois seront placées verticalement.
Pensez à imprimer les réglettes sur de grandes feuilles de 50 cm environ, car les chiffres sont petits.
- Mais comment si mon imprimante est au format A4 ??
- Et bien c'est simple ! Il vous suffit de découper dans une grande feuille de papier (de qualité) une feuille plus petite de 21 cm de largeur par 50 cm de longueur. Ensuite dans les paramètres d'impression de votre imprimante vous définissez votre nouveau format.
Je vous laisse un petit peu réfléchir pour le reste ... mais n'hésitez pas à me contacter (@)
Lisez aussi l'article de Stephan Weiss !
B) Remarks on Didier Roth's "Multiplicateur et diviseur à réglettes" / Stephan Weiss
"One of the problems while constructing a mechanical multiplying machine or instrument in the past had to do with the tens carry. Here we only discuss the tens carry mechanism in a multiplying instrument, which means there are no gears to perform this task.
During multiplication we first have to find the partial products out of every figure of the multiplicand and the – let's assume – only figure of the multiplier. Next we write down the unit figure of the partial product of lowest order, add its tens figure ....." (Download the article by Stephan Weiss (.pdf ))
---------------
*1
"Ce procédé n'a pu être exécuté que pour une transmission concernant deux chiffres, et dès que la transmission devrait s'opérer sur la 3e colonne de chiffre, les découpures montreraient des chiffres rouges qui indiquent une unité de plus suivant son rang, à ajouter à la colonne suivante"/ Roth, mars 1844*2
"Si l'on avait à effectuer le produit d'un nombre quelconque posé dans la première rainure horizontale inférieure par une multiplicateur composé de deux chiffres, on poserait d'abord le produit [...] donné par le 1er chiffre du multiplicateur, sur un papier à part, on écrirait également le produit du même nombre par le deuxième chiffre du multiplicateur, et ainsi de suite, si le multiplicateur contenait plus de deux chiffres, puis l'on ferait la somme des différents produits écrits; et la multiplication se trouverait ramenée à une addition; de même pour diviser un nombre par un autre, le résultat se bornerait à une soustraction"
www.ami19.org
Valéry Monnier
2011