|
||||
The machines of Doctor Roth (1800-1885) |
||||
Stephan Weiss
*English version by Eric Schurmann, November 2008*
Roth gives details here of a multiplier which is much simpler and cheaper than his superb variable toothed circular multiplier.
He has added to each dial of his adder gear trains which form a series of continuous gearings.
Above each dial, 8 other dials are arranged vertically and linked mechanically by pinions so that these turn in the same direction and which have a particularity in that their speed increases progressively by one tenth from bottom to top.
In short, when the top dial (of 9's) has completed a turn, the 8's dial will have done 2, etrc. and the adder (totaliser) dial will have done 9.
Since this one has a carry, the result obtained will be 81.
No complete prototype of this machine has been found so far but the CNAM has a small piece of one. Even if it is incomplete and if certain bits have been badly put back together, one can glean a very accurate idea of the machine.
Imagine it with a capacity of 8 figures. It would then have 72 dials!!! which would not be simple to manufacture.
For each decade there would be 9 dials. The lower one is the totaliser dial of the adder. The others correspond to the multiples 2,3,4,5,6,7,8, and 9.
Under the plate and for each multiple there is a 20 toothed dial wheel, armed with a jumper spring, and carrying the numbering 0.1.2.3.4.5.6.7.8.9. 0.1.2.3.4.5.6.7.8.9, two gear wheels with 90 teeth placed one above the other for the 9's multiple, two 80 toothed wheels for the 8's multiple, etc. These gear wheels were doubled up, probably for strength reasons. Intermediary pinions, also doubled up, have a number of teeth inversely proportional to the gear wheels in order to maintain an equal distance between each dial.
Michel Bardel's note:
"The problem with the 72 dial machine is that the effort required to turn the slowest dial is 38 times that for the fastest.
That explains why certain pinions had to be doubled up to withstand the effort. The theory of the conservation of work states that the product of the angle of rotation and the torque remains constant throughout the mechanism; therefore, if a wheel turns ten times more slowly, its torque is ten times greater. In the present case, one must add to the torque of the slowest wheel twice the torque of the following one, three times the next, then four times, etc…..the total being 38.
Unless the wheels turn with no effort, with the axles extremely well lubricated, that seems impracticable to me. And I'm not including the effort of the carrys which are also multiplied.
It was a foreseeable renunciation. It should not have gone any further.
B) Multiplier and divider with small rulers (5th addition)
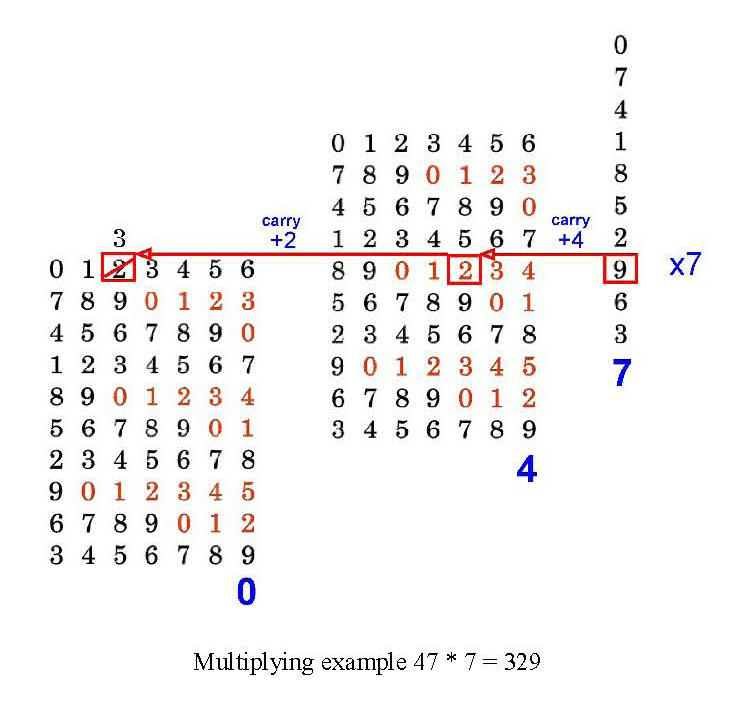
Roth imagined a very ingenious system for multiplying and dividing with small rulers. In this new setup, nine series of figures, one above the other, are printed on a small cardboard ruler. They show the multiple of each number from 1 to 9. The instrument, with a capacity of 6 figures, has 6 small rulers which overlap partially. Small, carefully positioned cutouts show "the excess of transmission of the unit on ten". In short, it's a matter of spreading the product of multiplying one figure by another over two orders of decimals. (*1)
The small rulers are placed in a wooden frame containing 9 horizontal windows (for each multiple).
The bottom section has six vertical slots with cursors which allow the small rulers to be moved up and down in order from 0 to 9.
If, for example, one introduces the number 123456, using the cursors, the window on the second level shows the product of 123456 multiplied by 2, i.e. 246912, the third level the product of 123456 by 3 or 370368 and so on up to the product of 123456 by 9 at the ninth level or 1111104. (*2)
B) Building of a replica
If the idea of building a replica is tempting, then here are some photos which will help you understand the principle. You only need to print six copies of the complete ruler which I have prepared. It will be necessary to stick the rulers on to some cardboard, strong but not too thick, because the rulers alone will bend and are likely to slip over one another under the pressure of the stylus. Assemble and constrain them by placing small strips of wood vertically. Try to print the rulers on sheets of paper about 50cm long, because the figures are small.
- But what if my printer only supports A4 format ?
- Simple! Just take a large sheet of (good quality) paper 50cm long and cut a strip narrower than 21cm from it. Then define this as a new format in the printing setup of your printer. I'll leave you a little while to think about the rest ... but don't hesitate to contact me (@)
Also read Stephan Weiss's article !"
(Height 50 cm)
B) Remarks on Didier Roth's "Multiplicateur et diviseur à réglettes" / Stephan Weiss
"One of the problems while constructing a mechanical multiplying machine or instrument in the past had to do with the tens carry. Here we only discuss the tens carry mechanism in a multiplying instrument, which means there are no gears to perform this task.
During multiplication we first have to find the partial products out of every figure of the multiplicand and the – let's assume – only figure of the multiplier. Next we write down the unit figure of the partial product of lowest order, add its tens figure ....." (Download the article by Stephan Weiss (.pdf ))
--------------
*1
"This procedure could only be used for an operation of two figures and, as soon as the operation had to act on the third column of figures, the windows showed red figures indicating that a further unit should be added to the following column" Roth, March 1844*2
"If one had to carry out a multiplication of a number entered into the bottom horizontal window by a multiplier composed of two figures, one would transcribe the product given by the first figure of the multiplier onto a separate piece of paper then one would write the product of the same number given by the second figure of the multiplier and so on if the multiplier consisted of more than 2 figures. Then one would add the various products and the multiplication would thus become an addition. The same thing for dividing a number by another, the result would be limited to a subtraction."*English version by Eric Schurmann, November 2008*
www.ami19.org
Valéry Monnier
2011