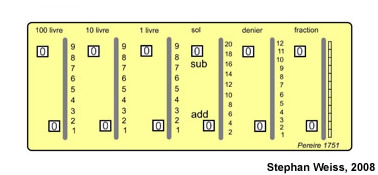
Notizen zur Rekonstruktion der Arithmetischen Maschine von Pereire 1750

[…]

Auszug aus den Registern der Königlichen Akademie der Wissenschaften, vom 5.Mai 1751

Auf Anordnung der Akademie haben wir eine von Herrn Pereire vorgestellte Rechenmaschine begutachtet, von dem unsere Gesellschaft schon die Methode für den Unterricht der Taubstummensprache zugelassen hatte.

Aus dem Bericht, den er der Akademie am 16. Dezember vorgetragen hat, zitiert Herr Pereire alles, was an Kenntnissen der diesbezüglichen Maschinen bekannt geworden ist, von denen diejenigen von Pascal, Perrault, Lépine und Boistissandeau den höchsten Rang einnehmen. Die erstere und die beiden letzten haben ein etwas störendes Volumen und sind aus einer Unmenge von Rädern, Federn, Haken und anderen Teilen zusammengesetzt, die sie teuer werden lassen, zu Reparaturen neigen und relativ unbequem zu bedienen sind.

Der Rabdologie-Abakus von Perrault ist viel einfacher, und es ist dieses Instrument, zu dem die Maschine von Herrn Pereire die meiste Beziehung hat. Dessen Abakus ist aus kleinen Stäben zusammengesetzt, bei denen jeder zwei übereinander stehende und durch einen Zwischenraum getrennte Ziffernspalten enthält. Die Ziffern der ersten Spalte enthalten in dieser Anordnung 0.1.2.3. bis 9 und die der zweiten Spalte die umgekehrte Anordnung 9.8.7. bis 0, und man bedient sie, indem man sie in ihren Schienen gleiten lässt. Sobald eine am unteren Ende ihres Gangs angelangt ist, findet ein im Inneren des Stabes zurückgezogener Haken eine Öffnung, rastet in eine auf der Seite des benachbarten Stabes angebrachte Vertiefung ein und verschiebt diesen um eine Einheit, um damit einen Zehnerübertrag für den ersteren zu markieren. Falls der Stab, der unten angekommen ist, im unteren Fenster keine Ziffer enthält, lässt man ihn nach oben gleiten, bis der Führungsstift an der Oberseite der Schiene ankommt: dann sieht man im unteren Fenster die Einheiten, welche zu den Zehnern gehören und die der Haken markiert hat, womit mehr oder weniger der Gebrauch dieses Instruments erklärt wäre.

Anstatt die beiden Ziffernspalten jedes Stabes übereinander anzuordnen, hätte Perrault sie Seite an Seite und eine etwas höher als die andere anbringen können, um sodann die oberen und unteren Fenster, in denen die Ziffern abzulesen sind, entsprechend anzulegen. Damit hätte der Abakus nicht mehr eine solche Länge gebraucht.

Die Maschine von Herrn Pereire folgt dieser Idee, ist aber noch einfallsreicher. Anstelle der Stäbe, bedient er sich kleiner Holzräder bzw. ganz flacher Zylinder, ähnlich der Spielsteine des Damespiels, alle auf einer Achse aufgereiht; die zylindrischen Oberflächen der Räder werden damit zu Stäbchen ohne Ende: er hat sodann den Umfang dieser Räder in dreißig gleiche Teile geteilt und dort zwei Ziffernreihen aufgetragen: die erste enthält dreimal die Zahlen 1.2.3.4.5.6.7.8.9.0 und die andere dreimal die Zahlen 0.9.8.7.6.5.4.3.2.1.

Von diesen Rädchen gibt es eines für den "Denier", eines für den "Sol", eines für die einfacheren und gewöhnlichen Brüche, wie 1/2, 1/3, 1/4, 1/6 usw. und sieben andere für die ganzen Zahlen, die Einheiten, Zehner, Hunderter, usw. bis zur Million: alle diese Rädchen zusammen bilden nichts anderes als einen Zylinder von drei Daumen Länge und 18 Linien Durchmesser, eingeschlossen in einem kleinen Kasten in der Form eines Koffers.

An der Oberseite des Kastens nehmen genauso viele Kerben wie Rädchen jede ein Drittel des Zylinderumfangs ein, d.h. Vertiefungen, mit denen man die Rädchen mithilfe eines Nadelstiftes drehen kann, in der gleichen Weise, wie man die Stäbe von Perrault verschiebt, indem man die gewünschte Ziffer von 1 bis 9 und 0 mitnimmt, mit dem Vorteil, dass die Ziffernspalten ohne Unterbrechung weitergehen und man also niemals die Rädchen zurückstellen muss, um die Ziffer der soeben durchgeführten Operation erscheinen zu lassen, wie es so häufig der Abakus von Perrault erfordert.

Herr Pereire hat den Umfang der Räder der Maschine in dreißig gleiche Teile eingeteilt, statt in zwanzig, damit die Kerben auf der Oberseite des Kastens nur ein Drittel des Umfangs des Zylinders einnehmen, anstatt der Hälfte, was nicht so bequem gewesen wäre.

Er hätte ihn auch in vierzig oder fünfzig gleiche Stücke teilen können, wobei die Öffnungen und Kerben zum Drehen der Räder nur 1/4 oder 1/5 des Umfangs eingenommen hätten; aber diese größere Anzahl der Einteilungen hätte viel größere Räder erfordert.

Außerdem befinden sich auf der Oberseite des Kastens, der die Räder enthält, zwei in Längsrichtung angebrachte Reihen von Fenstern, eine hinten am Kasten und die andere vorne: die erstere, um die Summe oder das Produkt verschiedener, zusammengezählter oder multiplizierter Zahlen zu finden, und letztere, um diejenige Zahl einzustellen, von der man eine andere abziehen will oder die man durch eine andere teilen will.

Das von Herrn Pereire erfundene Mittel zum Weiterdrehen eines Stellrades, jedes Mal, wenn es die Zehn überschreitet, ist höchst einfallsreich. Er hat hierzu auf der flachen Seiten jeden Rades dreißig Vertiefungen angebracht, die in etwa die Zähne eines Gegenrades darstellen. Auf der anderen planen Seite ist ein kleiner Hebel angebracht mit einem Haken an einem Ende und einer Abschrägung am anderen; jedes mal, wenn zehn Zahlen oder Einteilungen des Radumfangs vorbeigerückt sind, trifft die Abschrägung des Hebels auf einen feststehenden Zacken der Weißblechplatine zwischen beiden Rädern: dieser Zacken zwingt den Hebel an diesem Ende in das Innere des Rades einzudringen: der Haken auf der anderen Seite drängt heraus, geht durch eine dort angebrachte Öffnung in der Weißblechplatine, hakt sich in einen der 30 Zähne auf der Platte des Nachbarrades und zieht es einen Schritt weiter: danach befindet sich die Schrägung jenseits des Zackens und kehrt vermittels eines Federzugs an seinen Platz zurück: der Haken verbleibt im Innern des Rades und lässt, nachdem er es um den Wert eines Zahns weitergedreht hat, das benachbarte Rad in diesem Zustand.

Diese gesamte Einrichtung erscheint uns wohl überlegt, und uns bleiben nur noch zwei Bemerkungen übrig, die, wie wir glauben, die Aufmerksamkeit des Lesers verdienen:

1)Dass man vermittels der arithmetischen Maschine von Herrn Pereire ohne Tinte und Papier die vier fundamentalen arithmetischen Regeln durchführen kann, die ersten beiden für Livres, Sols und Derniers, sowie für sieben verschiedene Brucharten. Diese letztere Besonderheit der arithmetischen Maschine von Herrn Pereire, die speziell ihr eigen ist, ist umso mehr nützlicher, als man mit ihr die Brüche verschiedener Nenner mit der selben Leichtigkeit summieren und abziehen kann, als hätte man es mit ganzen Zahlen zu tun; man findet z.B. dass 1/4 1/3 3/8 5/24 ergeben 1 1/6 und dass davon 5/12 abgezogen den Wert 3/4 ergibt.

2)Auch wenn die arithmetische Maschine von Herrn Pereire, deren Umfang oben beschrieben wurde, nicht einen beträchtlichen Preis haben sollte, werden diejenigen, die sich eine anschaffen wollen, diesbezüglich urteilen, und - indem sie Herrn Pereire überzeugen – einen noch geringeren Preis herausschlagen, aufgrund des Nachfrageumfangs. Es ist wenig erstaunlich für die mechanischen Künste, dass sie mit einer solchen neuen Maschine sehr zufrieden wären, da diese an sich sehr geeignet ist, die Neugierde zu wecken und nicht nur für die Taubstummen von höchstem Nutzen ist, sondern insbesondere für alle diejenigen, die die Wissenschaft der Zahlen erfahren wollen.

Herr Pereire wohnt am Quai des Augustins, im Hotel d´Auvergne.

[…]

** Translation by Cris Stenella, 2008 **

Valéry Monnier
www.ami19.org
2011