Notes pour la reconstruction de la Machine arithmétique de Pereire, 1750 / Stephan Weiss 2008

[…]

Extrait des Registres de l’Académie Royale des Sciences, du 5 mai 1751
iLe journal des Sçavans, 1751,  pages 507-511

Nous avons examiné par ordre de l’Académie une machine Arithmétique, présentée par Mr Pereire, de la  Compagnie a déjà approuvé la méthode d’enseigner à parler aux Muets.
Mr Pereire cite dans le mémoire qu’il a lu à l’académie le 16 du mois de décembre dernier, tout ce qui est venu à la connaissance de machines faits à ce sujet, entre lesquelles celles de MM. Pascal, Perrault, de Lépine et de Boistissandeau, tiennent les premiers rangs. La première et les deux dernières, font d’un volume un peu embarrassant et composées de beaucoup de roues, ressorts, cliquets et autres pièces qui les rendent coûteuses, sujettes à réparation et d’un usage un peu incommode.
L’abaque rabdologique de M. Perrault, est beaucoup plus simple, et c’est à cet instrument  que la machine de M. Pereire a le plus de rapport. Cet abaque est composé de petites règles, contenant chacune deux colonnes de chiffres, l’une au dessus de l’autre, et séparées par une intervalle. Les chiffres de la première colonne font selon cet ordre, 0.1.2.3. etc. jusqu’à 9 et ceux de la seconde colonne dans un ordre inversé, 9.8.7 etc. jusqu’à 0, et l’on opère en faisant marcher ces réglettes dans les rainures qui les contiennent. Dès qu’elles arrivent au bas de leur marche, un cliquet qui est enfermé dans l’épaisseur de ces règles trouvant alors une ouverture qui lui permet d’engrener dans un cran de la règle voisine, la fait avancer d’un pas pour marquer une dizaine aux unités de la première, et si la règle qui vient d’arriver en bas, ne montre aucun chiffre à la fenêtre inférieure, on fait remonter la règle jusqu’à ce que la pointe qui la conduisait, arrive au haut de la rainure : on voit alors à la fenêtre d’en bas les unités simples qui doivent accompagner la dizaine que le cliquet a fait marquer, ainsi qu’il est plus au long expliqué dans l’usage de cet instrument.
Au lieu de mettre les deux colonnes de chiffres de chaque règle, l’une au dessus de l’autre, M. Perrault aurait pu les mettre l’une à côté de l’autre, en les mettant cependant l’une un peu plus haute que l’autre, et plaçant les fenêtres supérieures et inférieures, par lesquelles les chiffres paraissent, convenablement à cette disposition : par là l’abaque n’aurait plus eu besoin d’autant de longueur.
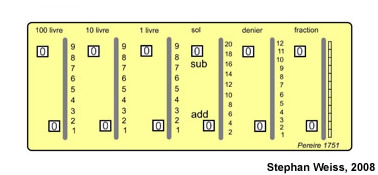
La machine de Mr Pereire tient de cette idée, mais elle est plus ingénieuse. Au lieu de règles, il se sert de petites roues de buis ou cylindres fort courts, comme des Dames de Trictrac, toutes enfilées par un même axe ; les surfaces cylindriques de ces roues ou Dames, deviennent par là des règles sans fin :  il a divisé la circonférence de chacune de ces roues en trente parties égales où il a écrit deux rangs de chiffres : le premier contient trois fois les nombres 1.2.3.4.5.6.7.8.9.0 et l’autre trois fois les nombres 0.9.8.7.6.5.4.3.2.1.
De ces roues, il y en a une pour les deniers, une pour les sols, une pour les fractions les plus simples et les plus ordinaires comme 1/2.1/3.1/4.1/6 etc. et sept pour les nombres entiers, unités simples, dizaines, centaines, etc . jusqu’aux millions : et toutes ces roues ensemble ne forment qu’un cylindre de trois pouces de long sur dix-huit lignes de diamètre, enfermé juste dans un petit coffret en forme de bahut.
Il y a au dessus de ce coffret autant de rainures que de roues occupant chacune le tiers de la circonférence du cylindre, par lesquelles on fait tourner les roues avec la pointe d’une aiguille, de la même manière qu’on fait marcher les règles de l’abaque de M. Perrault, en y prenant le chiffre qu’on veut depuis 1 jusqu’à 9 et 0, avec cet avantage que les colonnes des chiffres se succèdent ici sans interruption, on n’est jamais obligé de faire rétrograder les roues pour faire paraître le chiffre qui résulte de l’opération qu’on fait, comme l’exige souvent l’abaque de M. Perrault.
Mr Pereire a divisé la circonférence des roues de la machine en trente parties plutôt qu’en vingt, afin que les rainures qui sont au dessus du coffret, n’occupassent que le tiers de la circonférence du cylindre, au lieu qu’elles en auraient occupé la moitié, ce qui n’aurait pas été aussi commode.
Il aurait pu les diviser en quarante ou cinquante parties égales, et alors les ouvertures et rainures par lesquelles on fait tourner les roues n’auraient occupé que le ¼, ou la 1/5ème partie de la circonférence du cylindre ; mais ce plus grand nombre de divisions l’aurait obligé de faire les roues plus grandes.
Il y a de plus au dessus du coffret qui contient les roues, deux rangs de fenêtres dans le sens de la longueur l’un vers le derrière du coffret, et l’autre vers le devant : celles-ci pour y trouver la somme ou le produit de plusieurs nombres qu’on veut ajouter ou multiplier, et celle-là pour y mettre le nombre dont on en veut ôter un autre, ou qu’on veut diviser par un autre.
Le moyen qu’a imaginé M. Pereire pour faire avancer une roue d’une division toutes les fois que celle qui la précède marche de dix, est fort ingénieux. Il a fait pour cela sur un des côtés plats de chaque roue trente crans représentant à peu près les dents d’une roue de rencontre. L’autre face plane est réservée pour y loger une petite bascule, faite en crochet par un bout et en plan incliné par l’autre ; toutes les fois qu’on fait passer dix caractères ou divisions de la circonférence de cette roue, le plan incliné de la bascule rencontre un mentonnet fixe sur la platine de fer blanc qui est entre les deux roues : ce mentonnet oblige la bascule à s’enfoncer par ce bout là dans l’épaisseur de la roue : le crochet qui est de l’autre bout sort, passe à travers la platine de fer blanc par une ouverture qui y est pratiquée, accroche un des 30 crans qui sont sur le plat de la roue voisine et lui fait faire un pas : ce pas fait, le plan incliné se trouvant au-delà du mentonnet se remet à sa place par le moyen d’un ressort, le crochet rentre dans l’épaisseur de la roue et laisse dans cet état la roue voisine après l’avoir fait marcher de la valeur d’un cran.
Tout cet arrangement nous parait bien imaginé, simple et commode, et nous le jugeons digne d’approbation et d’être inséré dans le recueil des machines approuvées par l’académie.

[…]

Après ce que l’on vient de dire, il ne nous reste plus que deux choses dont nous avons cru qu’il était bon d’avertir nos lecteurs.

1°) Que par le moyen de la machine arithmétique de M. Pereire, on peut faire sans le secours de l’encre et du papier, les quatre règles fondamentales de l’arithmétique, les deux premières par livres, sols et deniers, ainsi que par sept différentes sortes de fractions. Cette dernière particularité de la machine arithmétique de M. Pereire qui lui appartient en propre, est d’autant plus utile, qu’on peut par son moyen additionner et soustraire les fractions de différents dénominateurs avec la même facilité que si l’on opérait avec des nombres entiers : on trouvera par exemple que 1/4 1/3 3/8 5/24 font 1 1/6 que si de cette somme on soustrait 5/12 il en reste 3/4.

2°) Quoique la machine arithmétique de M. Pereire dont le volume est marqué ci-dessus, ne soit pas d’un prix considérable, cependant si ceux qui voudront s’en procurer, jugent à propos d’en prévenir M. Pereire le prix sera encore moindre, à raison du nombre qu’on demandera. Il est peu de curieux pour les Arts mécaniques, qui ne qui ne soient bien aises d’avoir cette nouvelle machine, qui par elle-même est très propre à piquer la curiosité, et qui est fort utile non seulement pour les enfants muets, mais encore pour tous ceux qui veulent apprendre la science des nombres.
M. Pereire demeure Quai des Augustins, à l’Hôtel d’Auvergne.

[…]

Le journal des Sçavans, 1751,  pages 507-511

Valéry Monnier
www.ami19.org
2011